
Forma Polar y Forma Binomica PDF
Vamos a calcular el módulo y argumento del número z = 4 + 4 3 i. El complejo 4 + 4 3 i tiene por módulo: | 4 + 4 3 i | = 4 2 + ( 4 3) 2 = 16 + 16 ⋅ 3 = 16 + 48 = 64 = 8. porqué tanto la parte real como la imaginaria son positivas y por lo tanto el complejo vive en el primer cuadrante. De manera que para representarlo en forma polar este.

Conversión de un numero complejo de forma binomica a forma polar y
Expresar números complejos en forma polar y trigonómetrica. Matemáticas 1º de Bachillerato 12.1 Operaciones forma binómica . Formas de expresar números complejos. Ejemplos. Actividades interactivas. Resolver ecuaciones de 2º grado con soluciones complejas. Pasar de forma binómica a polar y viceversa. Números imaginarios puros. Opuesto.
Forma Binómica Polar Y Trigonométrica De Un Número Complejo Formă Blog
Tome el siguiente número complejo en forma rectangular. 1 − 3-√ i 1 − 3 i. Para convertir el siguiente número complejo de forma rectangular a forma polar trigonométrica, busque el radio usando el valor absoluto del número. r2 = 12 + (− 3-√)2 → r = 2 r 2 = 1 2 + ( − 3) 2 → r = 2. El ángulo se puede encontrar con.

COMPLEJO DE FORMA POLAR A BINÓMICA (EJEMPLO 1) YouTube
Ejemplo: Pasa a forma polar los siguientes números complejos: √3 es la tangente de 60 o y de 240 o .Observando la representación gráfica de z 1 o su afijo (1, √3) vemos que está en el primer cuadrante, por lo tanto el ángulo α es 60 o .-1 es la tangente de 135 o y de 315 o .Observando la representación gráfica de z 2 o su afijo (-2, 2)

Números complejos de forma polar a forma binómica YouTube
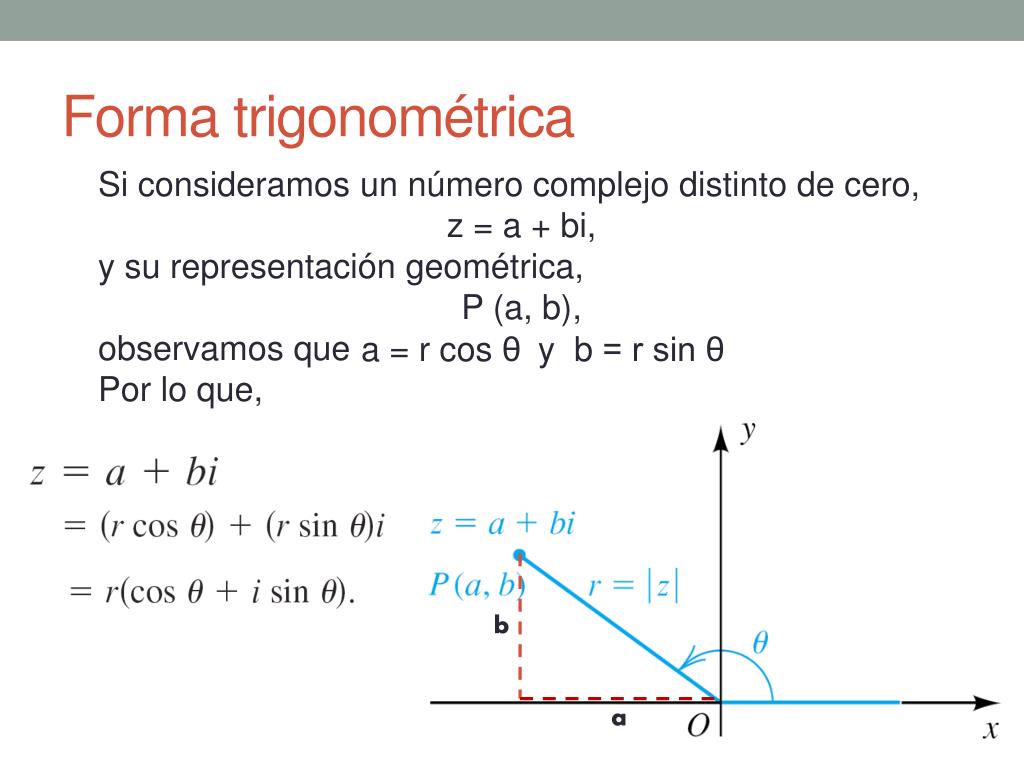
En la forma binómica, un complejo z se escribe como la suma de un número real a y un número real b multiplicado por la unidad imaginaria i: El número a es la parte real de z y b es la parte imaginaria de z. La forma trigonométrica del complejo z=a+bi es. El ángulo α que proporciona la función arcotangente es siempre entre -45° y 45°.

Expresar En Forma Binomica Un Numero Complejo Formă Blog
Ver más. Al igual que ocurre con los números naturales, los enteros o los reales es posible realizar operaciones con los números complejos en forma binómica tales como la suma, resta, multiplicación, etc. A continuación veremos las siguientes operaciones básicas: Suma y resta de números complejos. Producto de números complejos.

conversión de números complejos de su forma polar a binomica YouTube
La forma rectangular de un número complejo es una suma de dos términos: la parte real del número y la parte imaginaria del número multiplicada por i . Como tal, es realmente útil para sumar y restar números complejos. También podemos graficar un número complejo dado en forma rectangular en el plano complejo.

NÚMEROS COMPLEJOS. PASAR DE FORMA BINÓMICA A POLAR YouTube
La forma polar de un número complejo z = a + bi es , donde , , y para a > 0 o o para a < 0. Ejemplo : Exprese el número complejo en la forma polar. 5 + 2 i. La forma polar de un número complejo z = a + bi es . Así, primero encuentre el valor absoluto de r . Ahora encuentre el argumento θ . Ya que a > 0, use la fórmula .

Forma Binómica Polar Y Trigonométrica De Un Número Complejo Formă Blog
Calculadora 1: De forma binómica a polar. z1 = z 1 = + + ⋅i · i. Calcular. Para pasar de la forma binómica a la polar tenemos que calcular el módulo y el ángulo. Ejemplo: el complejo z = 2√3+2i z = 2 3 + 2 i en forma polar es 4π/6 4 π / 6.
Cual Es La Forma Binomica De Un Numero Complejo Formă Blog
Pasar de forma binómica a polar. Un número complejo en forma binómica tiene la forma a+bi a + bi. La forma polar es una expresión equivalente de este número escrito en función del módulo y el ángulo: r\angle\alpha r∠α. Los valores del módulo r r y el ángulo \alpha α pueden calcularse a partir de: r=\sqrt {a^2+b^2} r = a2 + b2.

Forma Polar Y Trigonometrica De Un Complejo Formă Blog
Forma binómica. Un número complejo Z (no confundirse con C, que es el conjunto al que pertenecen) se puede representar de la forma: Perteneciendo a y b al conjunto de los números reales. Esta forma de escribir los números complejos corresponde a la forma binómica, que tiene dos partes: a = Parte real. b = Parte imaginaria.

Números Complejos Operaciones en Forma Binomial (Forma Binómica
Solución. Dado que el Teorema de De Moivre se aplica a números complejos escritos en forma polar, primero debemos escribir (1 + i) en forma polar. Vamos a encontrar r. r = √x2 + y2 r = √()2 + ()2 r = √2. Entonces nos encontramos θ. El uso de la fórmula tanθ = y x da. tanθ = 1 1 tanθ = 1 θ = π 4.

EJEMPLO MULTIPLICACIONES ENTRE NÚMEROS COMPLEJOS DE LA FORMA BINÓMICA
Pasar el siguiente número complejo en forma binómica a forma polar: En primer lugar calculamos el módulo con la fórmula: Sustituimos «a» por -4 que es la parte real y «b» por 3, que es la parte imaginaria: Y operamos: El módulo es igual a 5. Ahora vamos a calcular el argumento, con la fórmula:

Números Complejos Convertir de forma Binómica a forma Polar y
El matemático y físico alemán Carl Friedrich Gauss (1777-1855) fué el primero en realizar una representación de los números complejos estableciendo que estos no se podían dibujar en una recta, como los reales, si no que se debían representar en un plano que denominó plano complejo.De esta forma, la parte real se puede representar en el eje de abcisas, también denominado eje real y la.

¿Cómo expresar un complejo en forma binómica, en forma polar (y
Un número complejo en forma binómica es a + bi.. El número a es la parte real del número complejo.. El número b es la parte imaginaria del número complejo.. Si b = 0 el número complejo se reduce a un número real, ya que a + 0i = a.. Si a = 0 el número complejo se reduce a bi, y se dice que es un número imaginario puro.. El conjunto de los números complejos se designa por .

Números complejos Pasar de forma polar a binómica y viceversa YouTube
En la forma binómica, un complejo z se escribe como la suma de un número real a y un número real b multiplicado por la unidad imaginaria i: El número a es la parte real de z y b es la parte imaginaria de z. La forma trigonométrica del complejo z=a+bi es. El ángulo α que proporciona la función arcotangente es siempre entre -45° y 45°.
- Saga El Rompecabezas Del Cabo Holmes
- Alumnos Inscritos Curso 2019 2020 Universidad De Gandia
- Pan De Espelta De Masa Madre
- Les Abeilles Mangent Le Miel
- Barril Brent 2 10 2018
- Aplicaciones Piratas Para Ver El Fútbol
- Autobus Ciudad De Mexico A San Luis Potosi
- Promoción De Empleo Joven 2018
- Casa De Arena Y Niebla Pelicula
- Receta Torta Fria Con Galleta Maria
