Coordenadas de un vector en una base ortonormal YouTube

suendo.best

️ Construir una BASE ORTONORMAL para SUBESPACIO H={ (x,y)∈R^2 / ax+by=0 }MÉTODO de Gram

Comencemos considerando una línea L, definida por el vector w = \twovec21, y un vector b = \twovec24 no encendido L, como se ilustra en la Figura 6.3.13. Figura 6.3.13. Encontrar la proyección ortogonal de b sobre la línea definida por w. Para encontrar \bhat, primer aviso que \bhat = sw para algún escalar s.

Cómo hallar una BASE ORTOGONAL y una BASE ORTONORMAL usando el Método de Gram Schmidt YouTube

Clases, SOLUCIÓN ejercicios, tareas, EXÁMENES resueltos, SOLUCIONARIOS https://linktr.ee/javi_profeCAPÍTULOS 1:22 una base para W6:30 Método de ortogonalizac.

CÓMO encontrar una BASE para un SUBESPACIO VECTORIAL Álgebra lineal Ejercicios RESUELTOS YouTube

Base ortogonal y base ortonormal. Decimos que B = { u →, v → } es una base ortogonal si los vectores que la forman son perpendiculares entre si. Es decir, u → y v → forman un ángulo de 90 ∘.

Coordenadas de un vector en una base ortonormal YouTube

Transcripción del video. hagamos un ejemplo más utilizando el proceso de grandes mid entonces digamos que tengo un espacio vectorial digamos el espacio vectorial generado por tres vectores y estos vectores van a vivir ahora en r 4 ok entonces tenemos el vector 0 0 1 1 tengo el vector digamos el 0 1 1 0 ok y voy a tener también un vector el 1.

Álgebra Linear Bases Ortonormais Exemplo YouTube

vimos en el último vídeo que si tengo una base [ __ ] normal vamos a partir como en los últimos vídeos de una base [ __ ] normal para un sub espacio bay si vamos a escribirlo del psuv espacio ve que el psuv espacio ve y si quiero hallar la proyección queremos hallar la proyección sobre sobre ese sube espacio ve de cualquier vector x que se encuentre en rn eso eso lo vimos ya en el vídeo.

Base ortonormal propiedades, ejemplos y ejercicios

TUTORÍAS, solución EJERCICIOS, trabajos y SOLUCIONARIOS de libros: https://linktr.ee/el_profe_javiCAPÍTULOS 1:19 Método de ortogonalización de Gram Schmidt12.

cómo hallar una base ortonormal de un espacio generado YouTube

Base ortonormal: propiedades, ejemplos y ejercicios. Una base ortonormal se forma con vectores perpendiculares entre sí y cuyo módulo además vale 1 (vectores unitarios). Recordemos que una base B en un espacio vectorial V, se define como un conjunto de vectores linealmente independientes capaces de generar dicho espacio.

Cómo hallar una BASE ORTOGONAL y una BASE ORTONORMAL usando el Método de Gram Schmidt YouTube

Encontrar la proyección en el subespacio con base ortonormal. Ejemplo.. encontramos un procedimiento para generar una base [ __ ] normal en el último vídeo y no fue un descubrimiento nuevo de hecho se llama el proceso de grandes mid pero vamos a aplicarlo ahora a ejemplos reales y con suerte veremos que es mucho más concreto que lo que.

Base ortonormal.

Una base ortonormal se forma con vectores perpendiculares entre sí y cuyo módulo además vale 1 (vectores unitarios).Recordemos que una base B en un espacio vectorial V, se define como un conjunto de vectores linealmente independientes capaces de generar dicho espacio.. A su vez un espacio vectorial es una entidad matemática abstracta entre cuyos elementos están los vectores, generalmente.

️ Cómo hallar una BASE ORTOGONAL y una BASE ORTONORMAL usando el Método de Gram Schmidt YouTube

Clases, SOLUCIÓN ejercicios, tareas, EXÁMENES resueltos, SOLUCIONARIOS https://linktr.ee/profe_javiCAPÍTULOS 0:52 una base para π4:37 Método de ortogonalizac.

Ejercicios resueltos base ortonormal

Base ortonormal. Ejemplos de bases ortogonal y ortonormal. El concepto de base es uno de los mas importantes en álgebra lineal. Básicamente una base es un subconjunto de elementos de nuestro espacio vectorial con la cual podemos expresar todos los vectores en términos de estos.Primero recordemos que tres vectores , y son linealmente.

Conjuntos ortogonales y ortonormales en R2 y R3 YouTube

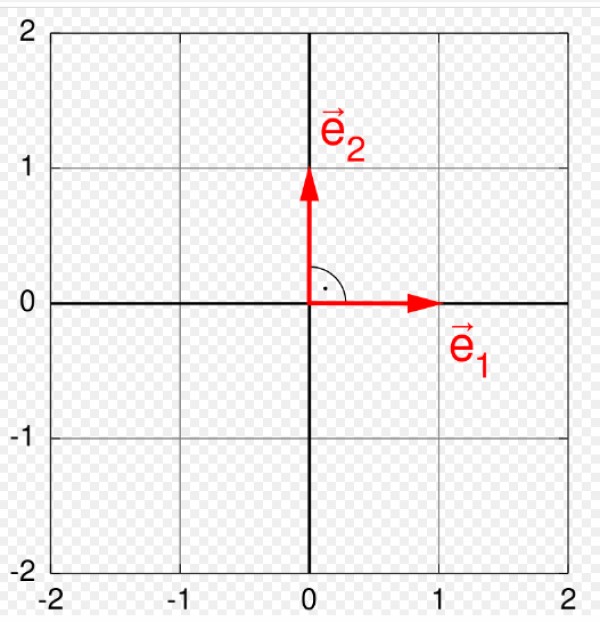
En otras palabras, que los vectores sean unitarios. $$$|\vec{u}|=\sqrt{1^2+0^2}=\sqrt{1}=1\quad |\vec{v}|=\sqrt{0^2+1^2}=\sqrt{1}=1$$$ Como podemos ver los dos vectores tienen módulo 1, es decir, son unitarios y por lo tanto, además de una base ortogonal también forman una base ortonormal. Solución: Forman una base ortogonal. No forman ni.

Cómo hallar una BASE ORTOGONAL y una BASE ORTONORMAL usando Método de Gram Schmidt

Sección 6.4 Encontrar bases ortogonales. La última sección demostró el valor de trabajar con conjuntos ortogonales, y especialmente ortonormales. Si tenemos una base ortogonal $\mathbf w_1,\mathbf w_2,\ldots,\mathbf w_n$ para un subespacio $W\text{,}$ la Fórmula de Proyección 6.3.15 nos dice que la proyección ortogonal de un vector $\mathbf b$ sobre $W$ es

Completar una base ortonormal YouTube

La definición de matriz ortogonal es la siguiente: Una matriz ortogonal es una matriz cuadrada con números reales que multiplicada por su traspuesta (o transpuesta) es igual a la matriz Identidad. Es decir, se cumple la siguiente condición: Donde es una matriz ortogonal y representa su matriz traspuesta. Para que esta condición se cumpla.

Bases ortonormales y proceso de ortonormalizacion

En un espacio Euclideano de dimensión n, un conjunto ortonormal de n vectores es una base ortonormal. La importancia de las bases ortogonales yace en que dada una base ortonormal B y un vector v, podemos encontrar varias propiedades de v en términos de B fácilmente. Por ejemplo, veremos más adelante que:

Ejemplo usando una matriz ortogonal de cambio de base para encontrar la matriz de transformació

sabemos que es una base [ __ ] normal pero la pregunta obvia que nos brinca es y para qué son buenas y una de las tantas respuestas a esa pregunta es que funcionan muy bien como existen sistemas de coordenadas o bases coordenadas entonces estos compadres aquí las bases orton normales son buenos son buenos sistemas sistemas de coordenadas de coordenadas ok entonces vamos a ver vamos a probar.